Vínculos

El enfoque de competencias en la educación.
·LA INNOVACIÓN: UNA PROBLEMÁTICA PERMANENTE EN EL CAMPO DE LA EDUCACIÓN
Necesitamos reconocer que la acelerada innovación se vuelve contra sí misma; desde una perspectiva interna a estos procesos —sobre todo en el ámbito tecnológico—, los ciclos de la innovación se acortan más cada vez. De esta manera, por ejemplo, un nuevo elemento en el ámbito de la informática tiene un periodo de frontera mucho más corto porque prácticamente es desplazado por otro de manera inmediata.
·TEMAS ESTRUCTURALES EN EL ÁMBITO PEDAGÓGICO FUNDAMENTALES PARA ACERCARSE AL ENFOQUE POR COMPETENCIAS
·EL ENFOQUE DE COMPETENCIAS EN EL CAMPO DE LA EDUCACIÓN Y DEL CURRÍCULO
Competencias disciplinares o transversales
En el caso de los planes de estudio, es factible reconocer diversas competencias que surgen de la necesidad de desarrollar esos conocimientos y habilidades vinculadas directamente a una disciplina, así como aquellas que responden a procesos que requieren ser impulsados por un trabajo que se realice desde un conjunto de asignaturas del plan de estudios.
Exploration on Student-Centered Fermentation Engineering Course by Problems Conducted Teaching
Fermentation engineering course is a strong application, practice of specialized course in the biological engineering professional. It is mass production of the required products process theory and an engineering technology courses, through microbial growth and metabolic activity and modern chemical technology. The content of the course are rich and various, and contain.

Si buscas
hosting web,
dominios web,
correos empresariales o
crear páginas web gratis,
ingresa a
PaginaMX
Por otro lado, si buscas crear códigos qr online ingresa al Creador de Códigos QR más potente que existe


VIRUS
Materia
Eratóstenes, nacido en Cirene en el año 284 antes de Jesucristo, y muerto en Alejandría a los 92 años, fue el primer científico de la historia de la Humanidad en medir con bastante precisión, la circunferencia de nuestro planeta.
Eratóstenes midió la circunferencia terrestre por primera vez con una gran exactitud, en una época en la que muy poca gente pensaba que el mundo no era plano como una mesa.

¿CÓMO MIDIÓ ERATÓSTENES?
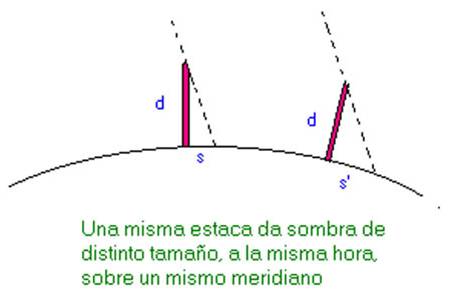
Figura 1
Pues, pensó, sencillamente, que dos estacas clavadas verticalmente en el suelo, a una distancia de varios kilómetros, sobre un mismo meridiano, darían sombras distintas a una misma hora en virtud de la curvatura de la superficie del planeta.
Los ángulos que forman los rayos de sol con la dirección de la estaca son:

Siendo s y s’ la sombra de cada estaca sobre la línea meridiana en cada lugar. La longitud de la estaca es d en ambos casos.
Si observamos ahora la figura 2 y nos fijamos en el triángulo que se forma, con ángulos a, a1 y 180-a2, donde a es el ángulo del arco de meridiano comprendido entre las posiciones que ocupan ambas estacas, y a1 y a2 son los ángulos que forman los rayos solares con la dirección de las estacas, vemos que, al sumar 180º los tres ángulos del triángulo es:
a1 + 180 - a2 + a = 180, es decir: a1 – a2 + a = 0, o sea: a = a2 – a1
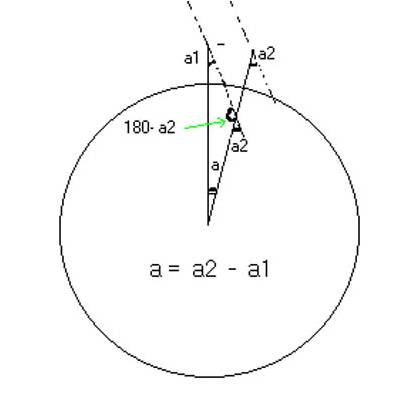
Figura 2
Conocido el ángulo a, y la longitud L del arco de meridiano entre ambos puntos de colocación de las estacas, será posible, mediante una sencilla regla de tres, encontrar la longitud total, X, de la circunferencia del planeta:
![]()
y, de aquí, el radio medio de la Tierra:
![]()
Si una de las dos estacas, en un determinado momento diera sobre la línea meridiana sombra nula, es decir, si en una de las estacas fuera cero el ángulo que forma la dirección de los rayos solares con la estaca, o, dicho de otra manera, si en uno de los dos lugares los rayos solares inciden perpendicularmente, entonces, se tendría que:
a1 = 0, por lo cual a = a2 – 0 = a2, es decir, el ángulo, a, que corresponde al arco de meridiano terrestre comprendido entre ambas posiciones de las estacas, es, precisamente el ángulo, a2, que formarían los rayos solares con la segunda estaca sobre la línea meridiana.
Este último hecho fue lo que utilizó Eratóstenes para hacer su medición.
Eratóstenes, que estaba en Alejandría, recordó que en un cierto día del año, en el solsticio de verano, los rayos solares caían verticalmente en la ciudad de Siena, situada en el mismo meridiano que Alejandría, pues recordaba que el sol se reflejaba en lo mas profundo de los pozos, a la hora del mediodía. Entonces, pensó que si media ese día en la ciudad de Alejandría, a la misma hora, el ángulo, a2, que los rayos solares formaban con la vertical, midiendo la sombra que sobre la línea meridiana formaba la estaca, conocería el ángulo del arco de meridiano entre Alejandría y Siena.
Eratóstenes midió la sombra sobre la línea meridiana producida por una estaca vertical en Alejandría, y conociendo la longitud de la estaca halló ese ángulo a la hora antedicha: resultó que el ángulo era de 7 grados (a2 = 7º). Ya sabia el ángulo del arco de meridiano entre Alejandría y Siena. Ahora faltaba conocer la distancia, a lo largo del meridiano, entre ambas ciudades, es decir, la longitud del arco L. Para ello Eratóstenes pagó a un hombre que hizo, a pié, tal medición. Eran, usando la medida usual en la época y en la zona, unos 4900 estadios, que equivaldría hoy ( a unos 6’125 estadios por kilómetro) a unos 800 kms.
Con estos datos ya es inmediato el cálculo:
Longitud de la circunferencia terrestre:
![]()
![]()
Radio medio del planeta:
![]()
Eratóstenes (284 a. J.C. - 192 a. J.C.)
(Cirene c. 284 (ó 276) a. J.C. - Alejandría c. 192 a .J.C.)
Astrónomo, geógrafo, matemático y filósofo de la antigua Grecia. Se le conoce por haber medido el perímetro de la Tierra. Educado en Atenas, fue invitado a Alejandría por Tolomeo III para que se hiciera cargo de la educación de su hijo Filopator. Allí se ocupó de la dirección de la gran biblioteca del museo hasta su muerte.
Tuvo fama de ser uno de los hombres más cultos de su tiempo, autor reputado en materias como la historia, la crítica literaria, la cronología o la teoría musical aunque, sobre todo, destacó como geógrafo y matemático. Su sabiduría le hizo merecedor del apelativo del Pentatlos, "el atleta completo". Sin embargo, en ninguno de los campos que cultivó fue considerado por sus contemporáneos como una figura de primera línea, por eso se le llamó "el beta" (algo así como el número 2). Su discípulo más famoso, Arquímedes, le dedicó su Método.
 Funciones Matematicas: Conceptos Basicos
Funciones Matematicas: Conceptos BasicosLas funciones matematicas, en terminos simples, corresponden al
proceso logico comun ue se expresa como “depende de”. Este proceso
logico se aplica a todo lo que tiene relacion a un resultado o efecto
sea este medible o no en forma cuantitativa.
Las funciones matematicas pueden referirse a situaciones cotidianas,
tales como: el valor del consumo mensual de agua potable que
depende del número de metros cúbicos consumidos en el mes; el valor
de un departamento que depende del número de metros cuadrados
construidos; la sombra proyectada por un edificio que depende de la
hora del día; el costo de una llamada telefónica que depende de su
duración; el costo de enviar una encomienda que depende de su peso;
la estatura de un niño que depende de su edad.
A modo de ejemplo, ¿cuál sería la regla que relaciona los números de la
derecha con los de la izquierda en la siguiente lista?:
1 --------> 1
2 --------> 4
3 --------> 9
4 --------> 16
Los números de la derecha son los cuadrados de los de la izquierda.
La regla es entonces "elevar al cuadrado":
x -------> x2.
Para referirse a esta regla podemos usar un nombre, que por lo general
es la letra f (de función). f es la regla "elevar al cuadrado el número".
Usualmente se emplean dos notaciones:
x --------> x2 ó f(x) = x2 .
Así, f(3) significa aplicar la regla f a 3. Al hacerlo resulta 32 = 9.
Entonces f(3) = 9. De igual modo f(2) = 4, f(4) = 16 f(a) = a2, etc.
Consideremos algunos ejemplos que constituyen funciones
matemáticas.
A) Correspondencia entre las personas que trabajan en una oficina y
su peso expresado en kilos
X Y
Marcela 55
Pablo 88
Sergio 62
Jorge 88
René 90
Cada persona (perteneciente al conjunto X) constituye lo que se llama la entrada o
variable independiente. Cada peso (perteneciente al conjunto Y) constituye lo que se
llama la salida o variable dependiente. Notemos que una misma persona no puede
tener dos pesos distintos . Notemos también que es posible que dos personas
diferentes tengan el mismo peso.
B) Correspondencia entre el conjunto de los numero reales (variable independiente)
y el mismo conjunto (variable dependiente), definida por la regla "doble del número
más 3".
x -------> 2x + 3
Algunos pares de números que se corresponden por medio de esta regla son:
X Y
-1 ------------> 1
0 -------------> 3
1 -------------> 5
2 -------------> 7
Estos ejemplos van introduciendo la noción de función: se pretende que todos y cada
uno de los elementos del primer conjunto están asociados a un y sólo a un elemento
del segundo conjunto. Todos y cada uno significa que no puede quedar un elemento
en X sin su correspondiente elemento en Y. Un y sólo a un significa que a un mismo
elemento en X no le puede corresponder dos elementos distintos en Y.
Ahora podemos enunciar la siguiente definición formal:
Una función f es una regla que asigna a cada elemento x de un conjunto X
exactamente un elemento, llamado f(x) de un conjunto Y.
Otra definición equivalente es: sean X e Y dos conjuntos. Una función de X en Y
es una regla (o un método) que asigna un (y sólo un) elemento en Y a cada elemento
en X.

Copyright mi página Web
![]()
![]()
![]()
![]()
![]()

